1. 신경망
- 인공 신경망: 생물학적인 신경망에서 영감을 받아서 만들어진 컴퓨팅 구조이다.
- 생물학적인 신경망에서 수학적인 구조로 모델링 한 것
- 퍼셉트론:
- 신경망(딥러닝)의 기원이 되는 알고리즘
- 퍼셉트론(인공 뉴런): 다수의 신호를 입력으로 받으면 Activation function(활성화 함수)를 거쳐 특정 하나의 신호를 출력.
2. 뉴런을 사용한 논리 연산
- 생물학적 뉴런에서 착안한 매우 단순한 신경망 모델임
- A,B는 input
- 첫번째 네트워크는 항등함수. (뉴런 A가 활성화 되면 뉴런 C도 활성화 된다.)
- 두번째 네트워크는 논리곱 연산을 수행. (뉴런 A,B 모두 활성화 될때만 뉴런 C가 활성화 됨.)
- 세번째 네트워크는 논리합 연산을 수행. (뉴런 A, B 둘 중 하나라도 활성화 되면 C가 활성화 된다.)
- 네번째 네트워크는 뉴런 B가 켜저있지 않고 A가 켜질 때 활성화 된다. (뉴런 B의 입력이 뉴런 C의 활성화를 억제할 수 있음.)

3. 퍼셉트론의 신호
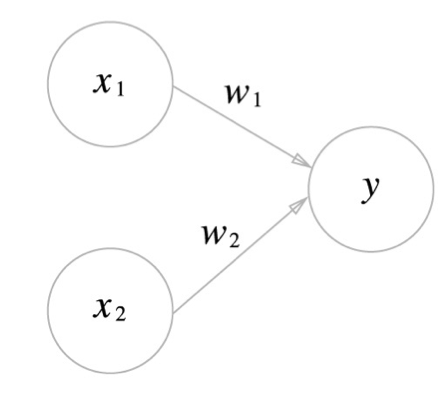
- 신호 : 흐른다(1), 흐르지 않는다(0) 두 가지 값을 가진다.
- x1, x2 : 입력 신호
- w1, w2 : 가중치
- 가중치(weight)는 입력 신호가 결과 출력에 주는 영향도를 조절하는 매개 변수
- 입력신호가 y 뉴런에 보내질때 각각 고유한 가중치가 곱해짐 ( w1 * x1 , w2 * x2 )
- 퍼셉트론에서는 가중치가 클수록 강한 신호를 흘림.
- 뉴런의 활성화 : 뉴런에서 보내온 신호의 총합이 정해진 한계(임계값)를 넘어설 때만 1을 출력
- 임계값 : 정해진 한계 뉴련의 활성화를 결정짓는 값.
- 뉴런에서는 입력 신호의 가중치 합이 어떤 입계값을 넘는 경우에만 뉴런이 활성화 되어서 1을 출력함. 그렇지 않으면 0을 출력함.
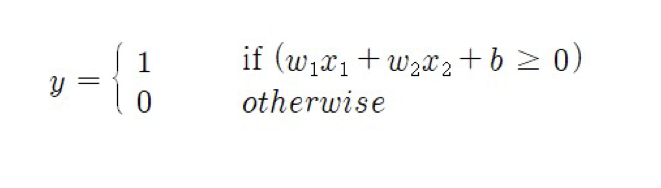
* b: bias(편향), 절편을 의미. 뉴런이 얼마나 쉽게 활성화 되느냐를 조정.
-편향값이 높으면 높을수록 분류의 기준이 엄격하다는 것을 의미함.
-반대로 편향이 낮을 수록 한계점이 낮아 데이터의 허용 범위가 넓어지는 만큼 학습 데이터에만 잘 들어맞는 모델일 만들어질 수 있음(과대 적합).
-허용 범위가 넓어지는 만큼 필요 없는 노이즈가 포함될 가능성도 높다. (30 이하의 값들을 노이즈라고 한다면 바이어스가 선언되어 있지 않다면 이 모든 노이즈들을 수용하게 됨. 반대로 바이어스가 미리 지정되어 있어 30 이상의 값들을 무시해 줄 수 있음.)
4. 퍼셉트론 학습 알고리즘
- 학습이라고 부르려면 신경망이 스스로 가중치를 자동으로 설정해 주는 알고리즘이 필요하다. 퍼셉트론에서도 학습 알고리즘이 존재한다.
input : 학습 데이터 (x^1, d^1),......,(x^m,d^m)
1) W 와 bias를 0 또는 작은 난수로 초기화
2) while ( 가중치가 변경되지 않을 때까지 반복 / 모든 데이터에 대해 에러가 없을 경우 종료)
3) for x^k,d^k in zip(x,d)
4) y(t) = f(w(t) * x^k) --> 지정된 가중치와 주어진 학습데이터로 출력값(예측값) 얻기
5) 다음 가중치 W에 대하여 W(t+1) = W(t) + (실제값-출력값)*학습률*x^k
실제값은 1과 0 총 두개의 값을 가진다고 하였을때,
퍼셉트론이 1을 0으로 잘못 식별했다고 한다면, 가중치의 변화량은 (1-0)*학습률*x^k이 된다.(가중치 증가, 출력값을 1로 유도)
반대로 0을 1로 잘못 식별했다고 한다면, ,가중치의 변화량은 (0-1)*학습률*x^k 이된다. (가중치 감소, 출력값을 0으로 유도)
5. 파이썬으로 다양한 논리 회로 구현
1)AND 게이트
def AndGateThreshold(x1,x2):
"""
출력값을 임계값을 통해 분류하는 AND게이트
"""
w1, w2, theta = 0.5,0.5,0.7 #가중치1,2 임계값
tmp = x1*w1 + x2*w2 #출력값 계산
if tmp <= theta: #출력값이 임계값보다 작거나 같다면 0을 리턴
return 0
elif tmp > theta: #출력값이 임계값보다 크다면 1을 리턴
return 1
def AndGateWB(x1,x2):
"""
출력값을 지정한 가중치와 바이어스로 계산하여 0을 넘기는지 아닌지를 분류하는 AND게이트
"""
x = np.array([x1,x2]) #입력 데이터 np array 형태로 저장.
w = np.array([0.5,0.5]) #입력 데이터에 대한 가중치 지정.
b = -0.7 #Bias 지정
tmp = np.sum(w*x) + b #입력 데이터를 가중치와 바이어스로 가공한 출력값 계산
if tmp <= 0: #출력값이 0보다 작거나 같다면 0을 리턴
return 0
else : # 출력값이 0보다 큰 수라면 1을 리턴
return 12) OR 게이트
- AND게이트와 코드는 매우 유사하지만 bias와 Weight 값만 다름.
def ORGate(x1,x2):
x = np.array([x1,x2 ])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 13) NAND 게이트
- AND게이트와 코드는 매우 유사하지만 bias와 Weight 값만 다름.
def NAND_Gate(x1,x2):
"""
NAND GATE 두개의 입력값이 모두 활성화 되면 0 / else 1
"""
x = np.array([x1,x2 ])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
5. 퍼셉트론의 한계
- 먼저 단층 퍼셉트론 학습 알고리즘은 선형 분류밖에 하지 못한다는 한계를 가지고 있다.
- 즉 AND, OR 문제는 선형으로 문제를 해결했으나, XOR 같은 문제는 해결할 수 없다는 의미이다. 따라서 다층 퍼셉트론과 활성화 함수 sigmoid와 같은 비선형 함수를 통해 해결할 수 있다.
'ML > 지도학습' 카테고리의 다른 글
| 로지스틱 회귀(Logistic Regression) (0) | 2022.10.18 |
|---|---|
| 회귀 모델 평가 (0) | 2022.10.17 |
| 1.선형 회귀(Linear Regression) (0) | 2022.10.12 |


