1. 회귀
- 회귀는 주어진 입력- 출력 쌍을 학습한 후, 새로운 입력값이 들어왔을 때 합리적인 출력 값을 예측하는 것.
-회귀에서 학습시키는 데이터는 이산적이지 않고 연속적이다. (입력과 출력이 모두 실수이다.)
- 이산적 : 변수가 취할 수 있는 값의 수가 유한한 경우, 정수로 표시된 자료 --> 일정 기간 동안 교통사고 발생건수, 특정 가구의 자녀수
- 연속적 : 체중, 거리, 시간 과 같이 무한히 작은 단위로 측정이 가능하여 모든 실수 값을 취할 수 있는 자료. --> 무게, 온도, 부피
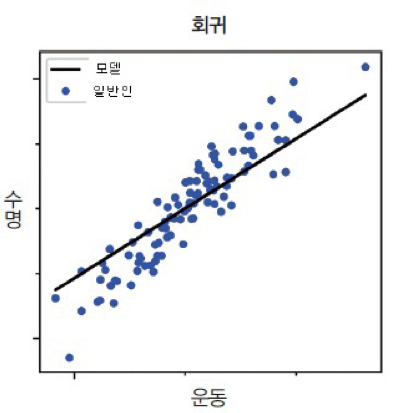
결국 회귀는 입력(x)와 출력(y)가 주어질 때, 입력에서 출력으로의 매핑 함수를 학습하는 것이라고 할 수 있다.
2.선형 회귀 소개
- 직선의 방정식 : f(x) = mx+b
- 선형 회귀는 입력 데이터를 가장 잘 설명하는 기울기의 절편 값을 찾는 문제임.
- 선형 회귀의 기본식: f(x) = Wx + b
- 기울기 -> 가중치(W)
- 절편 -> 바이어스(b)
3. 선형 회귀의 종류
- 단순 선형 회귀 : 독립변수 ( x ) 가 하나인 선형 회귀
- 다중 선형 회귀 : 독립 변수가 여러개인 경우
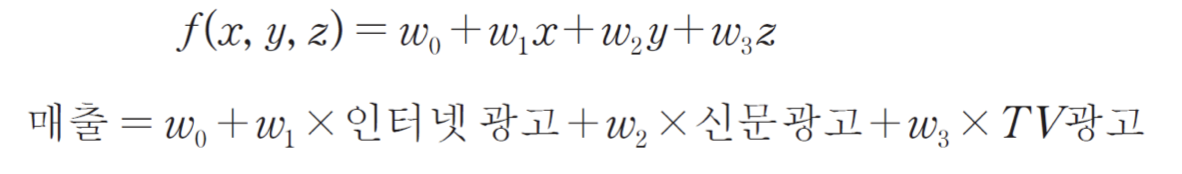
선형 회귀 실습
1.데이터 가공
import matplotlib.pyplot as plt
import pandas as pd
#데이터 읽어오기
dataset = pd.read_csv('LinearRegressionData.csv')
#독립 변수, 종속 변수 분리
X = dataset.iloc[:,:-1].values # 처음부터 마지막 컬럼 직전까지의 데이터(독립 변수-원인)
y = dataset.iloc[:,-1].values # 마지막 컬럼 데이터(종속 변수 - 결과)
#데이터 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # 훈련 80 : 테스트 20 으로 분리2.데이터 학습
from sklearn.linear_model import LinearRegression
reg = LinearRegression() # 모델 생성
reg.fit(X_train,y_train) # 학습 모델생성
3.학습한 모델을 통해 독립변수 X에 대한 예측값 출력하기.
y_pred = reg.predict(X) # 이전 학습한 모델을 통해 독립변수 X에 대한 예측값을 y_pred 에 저장
y_pred
4.학습한 모델 시각화
plt.scatter(X,y, color='blue') # 산점도 그래프
plt.plot(X,y_pred, color='green') # 선 그래프, 학습한 모델을 통해 X에 대한 예측값을 선 그래프를 통해 나타냄.
plt.title('Score by hours') # 제목
plt.xlabel('hours') # X 축이름
plt.ylabel('score') # y 축이름
plt.show()
5.학습한 모델의 기울기, 바이어스 값 출력하기.
reg.coef_ # 기울기 값을 출력함
reg.intercept_ # y절편을 출력4. 손실함수 ( MSE : Mean Square Error)
- 직선과 데이터 사이의 간격을 제곱하여 합한 값을 손실 함수 또는 비용 함수라고 한다.

- 장점: 실제 정답에 대한 정답률의 오차뿐만 아니라 다른 오답에 대한 정답률의 오차도 포함하여 계산해 준다.
- 단점 : 값을 제곱하기 때문에 절댓값이 1 미만인 값은 더 작아지고, 1보다 큰 값은 더 커지는 왜곡이 발생, 제곱하기 때문에 노이즈 값(확 튀는 값)의 영향을 많이 받음.
5. 경사 하강법 ( Gradient Descent Method)
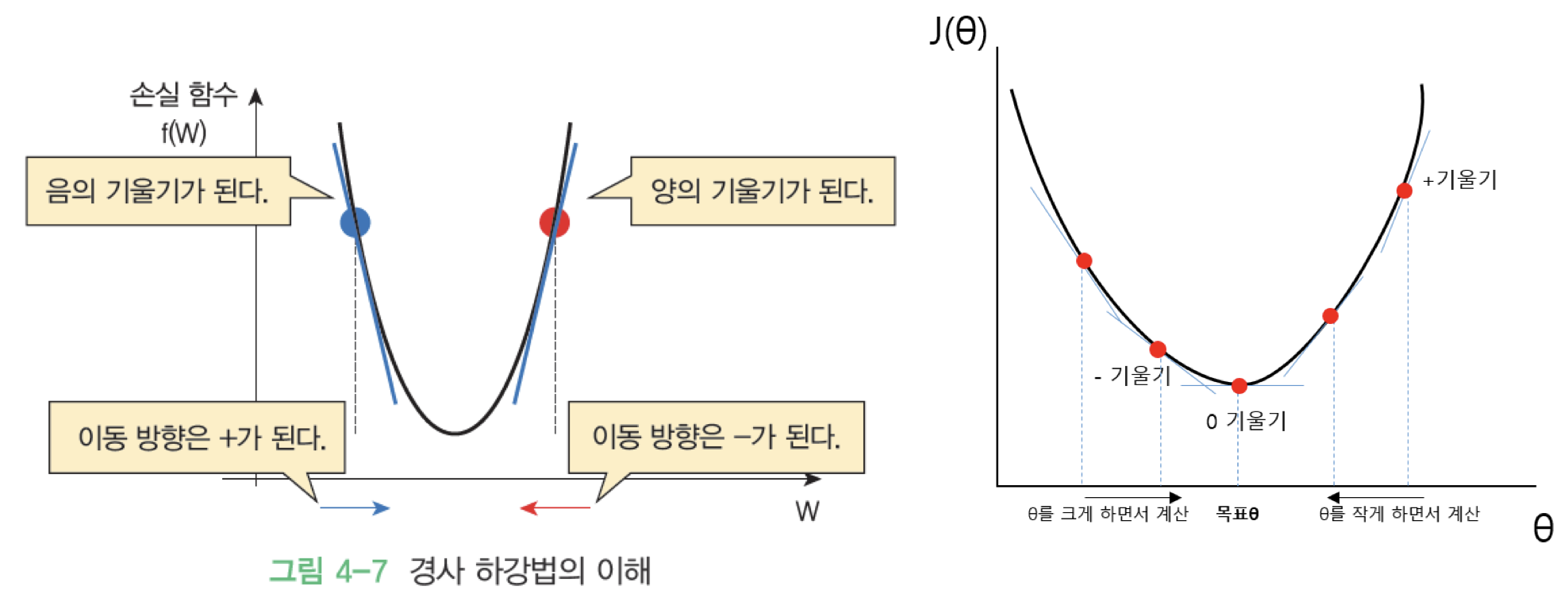
-함수 값이 낮아지는 방향으로 독립 변수 값을 변형시켜가면서 최종적으로는 최소 함수 값을 갖도록 하는 독립 변수 값을 찾는 방법이다.
-경사 하강법에서는 학습 시 스텝의 크기(step size)가 중요하다. 이를 학습률이라고 한다.
- 학습률이 너무 낮을 경우 알고리즘이 수렴하기 위해 반복해야 하는 값이 많으므로 학습 시간이 오래 걸린다.
- 그리고 지역 최솟값(local minium)에 수렴할 수 있다.
-반대로 학습률이 너무 클 경우 학습 시간은 적게 걸리나, 스텝이 너무 커서 전역 최소값(global minimum)을 가로질러 반대편으로 건너뛰어 최솟값에서 멀어질 수 있다.

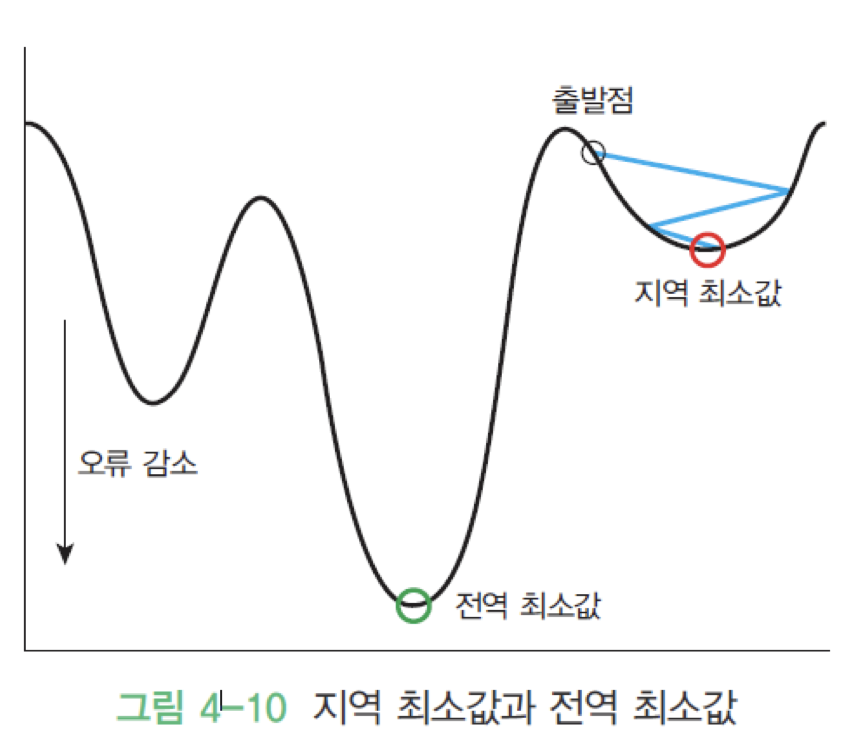
일반적으로 0.001, 0.003, 0.01, 0.03, 0.1, 0.3 의 값을 사용한다.
* 하지만 경사 하강법에서는 전체 데이터를 모두 사용해서 기울기를 계산하므로 데이터가 많을 경우 그만큼 시간이 많이 걸리며, 전역 최솟값이 아닌 지역 최솟값에 빠지기 쉽다.
5. 확률적 경사 하강법 ( SGD, Stochastic Gradient Descent Method)
-경사 하강법은 전체 데이터를 모두 사용해서 기울기를 계산하기 때문에 학습하는데 많은 시간이 필요함. -> 학습 데이터가 큰 경우 부담이 있음.
- 이러한 점을 보완하기 위해 확률적 경사 하강법을 사용함.
- 매 step에서 딱 한개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 기울기 계산.
특징
- 매우 적은 데이터를 처리하기에 학습 속도가 빠름.
- 하나의 샘플만 메모리에 있으면 되기 때문에 큰 데이터셋도 학습 가능
- 샘플의 선택이 확률적(Stochastic)이기 때문에 배치 경사 하강법에 비해 불안정
- cost funciton이 local minimum에 이를 때까지 부드럽게 감소하지 않고 위아래로 요동치며 평균적으로 감소.

Epoch
- 훈련 데이터셋에 포함된 모든 데이터들이 한 번씩 모델을 통과한 횟수, 모든 학습 데이터셋을 학습하는 횟수
- Epoch를 높일수록, 다양한 무작위 가중치로 학습을 해보는 것이므로 적합한 파라미터를 찾을 확률이 높아짐. --> 손실 값 이 내려감.
- 지나치게 Epoch를 높이게 되면, 그 학습 데이터셋에 과적합(overfitting) 되어 다른 데이터에 대해선 제대로 된 예측을 하지 못할 수 있음.

- 훈련 세트 정확도는 에포크가 진행될 수록 꾸준히 증가하는 반면, 테스트 세트 점수는 어느 순간 감소하기 시작함
- 이 시점 모델이 과대적합되기 시작하는 곳.
- 과대 적합이 시작하기 전에 훈련을 멈추는 것을 조기 종료(early stopping)이라고 함.
-에포크 과대 적합
- 에포크 횟수가 많으면 훈련된 모델은 훈련 세트에 너무 잘 맞아 테스트 세트에는 오히려 점수가 나쁜 과대적합 모델일 가능성이 높음.
-에포크 과소 적합
- 에포크 횟수가 적으면 훈련된 모델은 훈련 세트와 테스트 세트에 잘 맞지 않은 과소적합된 모델일 가능성이 높음.
확률적 경사 하강법 실습
1. 데이터 가공
import matplotlib.pyplot as plt
import pandas as pd
#데이터 읽어오기
dataset = pd.read_csv('LinearRegressionData.csv')
#독립 변수, 종속 변수 분리
X = dataset.iloc[:,:-1].values # 처음부터 마지막 컬럼 직전까지의 데이터(독립 변수-원인)
y = dataset.iloc[:,-1].values # 마지막 컬럼 데이터(종속 변수 - 결과)
#데이터 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) # 훈련 80 : 테스트 20 으로 분리2. 확률적 경사 하강법 모델 불러오기 및 데이터 학습
from sklearn.linear_model import SGDRegressor # SGD : Stochastic Gradient Descent 확률적 경사 하강법
sr = SGDRegressor()
sr.fit(X_train, y_train)3. 데이터 시각화
plt.scatter(X_train, y_train, color='blue') # 산점도
plt.plot(X_train, sr.predict(X_train), color='green') # 선 그래프
plt.title('Score by hours (test data, SGD)') # 제목
plt.xlabel('hours') # X 축 이름
plt.ylabel('score') # Y 축 이름
plt.show()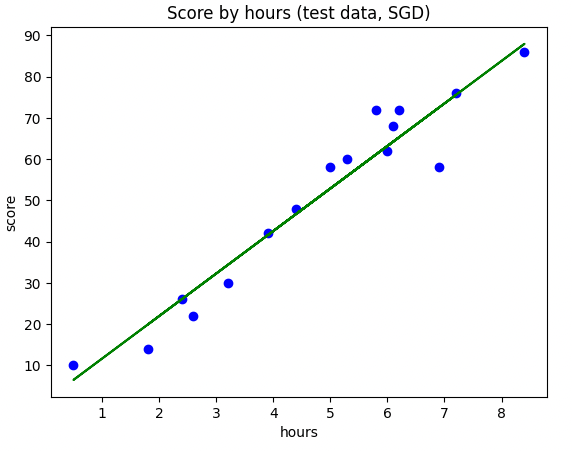
SGDRegressor() 옵션
- max_iter : 훈련 세트 반복 횟수 (Epoch 횟수)
- eat0 : 학습률
- 지수 표기법 -> 1e-3 : 0.001 ( 10^-3) , 1e-4 : 0.0001
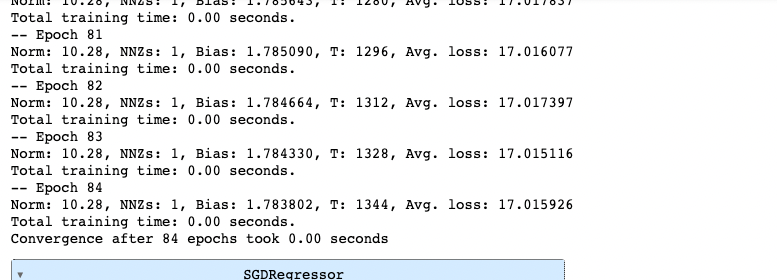
-verbose : 훈련세트를 반복하며 손실이 얼마나 줄어들지를 보여주는 옵션
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.SGDRegressor.html
sklearn.linear_model.SGDRegressor
Examples using sklearn.linear_model.SGDRegressor: Prediction Latency Prediction Latency SGD: Penalties SGD: Penalties
scikit-learn.org
from sklearn.linear_model import SGDRegressor # SGD : Stochastic Gradient Descent 확률적 경사 하강법
sr = SGDRegressor(max_iter =100, eta0 = 0.0001, random_state=0, verbose=1)
sr.fit(X_train, y_train)
'ML > 지도학습' 카테고리의 다른 글
| 로지스틱 회귀(Logistic Regression) (0) | 2022.10.18 |
|---|---|
| 회귀 모델 평가 (0) | 2022.10.17 |
| 퍼셉트론(단층) (0) | 2022.10.17 |


