에지 검출 (Edge Detection) / Image Gradients
에지 검출의 기초
- 물체 내부나 배경은 변화가 없거나 작은 반면, 물체 경계는 변화가 크다.
- 에지란 영상의 명암, 컬러, 또는 텍스처와 같은 특성이 급격히 변하는 지점이다
- 이 원리에 따라 에지 검출 알고리즘은 명암, 컬러, 또는 텍스처의 변화량을 측정하고, 변화량이 큰 곳을 에지로 검출한다.
- 변화량을 구하기 위해 보통 도함수(derivative)를 사용하는데, 컴퓨터 비전에서는 연속 공간이 아닌 이산 공간에서 정의된다.
- 영상에서는 데이터가 일정간격으로 나열되어 있기 때문에 수학적인 미분 연산을 하지 않는다
- 대신 인접한 화소끼리의 차이를 취하는 연산을 한다.
에지 모델과 연산자
- 다음 그림은 계단 에지(step edge)와 램프 에지(ramp edge)라 불리는 두 종류의 에지를 가진 영상이다.
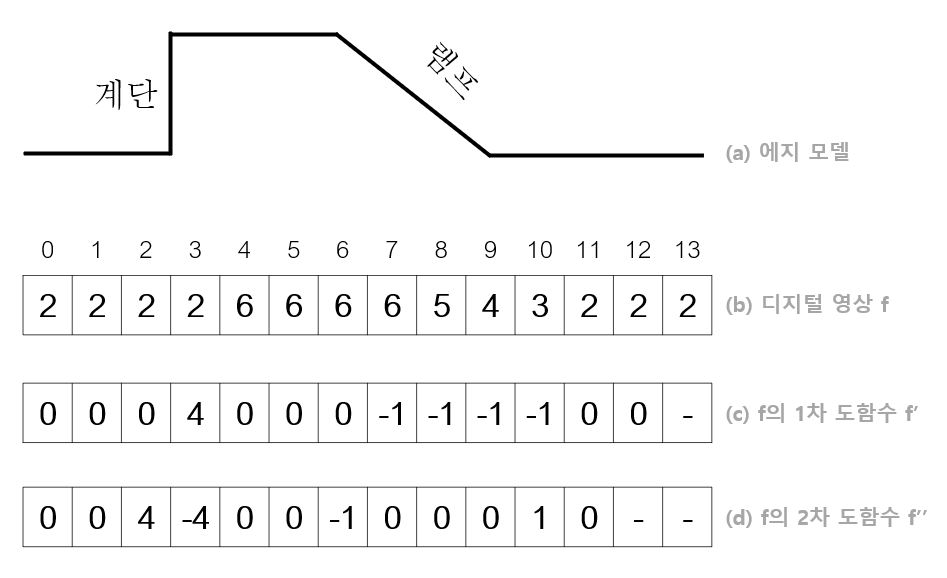
- 1차 미분을 진행한 그림 c를 살펴보면 계단 에지에서 봉우리(Peak)가 나타난다. 봉우리의 두께가 1이므로 계단에지만 존재하는 경우, 에지를 찾는 일이 매우 간단하다.
- 하지만 실제 데이터에서는 카메라로 영상을 획득할때 완벽하게 초점을 맞추기 불가능하기 때문에 주로 램프에지가 나타난다.
- 위 그림에서 7부터 10에 걸처 램프 에지가 나타난 두께가 4이다.
- 에지의 정확한 위치를 찾는 일을 Localization이라고 한다.
- 램프에지와 계단 에지 모두 1차 미분 결과로 봉우리가 나타나고, 2차 미분 결과에서 영교차(zero crossing)이 나타난 것을 볼 수 있다.
- 이렇게 봉우리와 영교차를 찾는 것이 에지 검출의 기본 원리이다.
영교차(zero crossing)이란?
- 영교차는 수학 함수의 부호가 변하는 지점으로, 함수 그래프에서 축의 절편으로 표시된다.
- 전자, 수학, 음향 및 이미지 처리에서 일반적으로 사용되는 용어입니다.
- 수학에서 영교차는 양수에서 음수, 또는 음수에서 양수로 변화가 일어나는 곳을 일컫습니다.
- 전자제품에서의 영교차는 전압이 0이 되는 지점을 감지하는 장치를 말합니다.
- 디지털 명령 제어 유형 시스템과 같은 교류 회로를 통해 데이터를 전송하는 시스템에서 중요한 역할을 합니다.
- 현실에서는 잡음이 발생하여 에지 연산자를 제거하기 전 스무딩 연산을 적용해야 한다.
- 아래 그림은 에지 검출에 쓰는 여러가지 마스크이다.
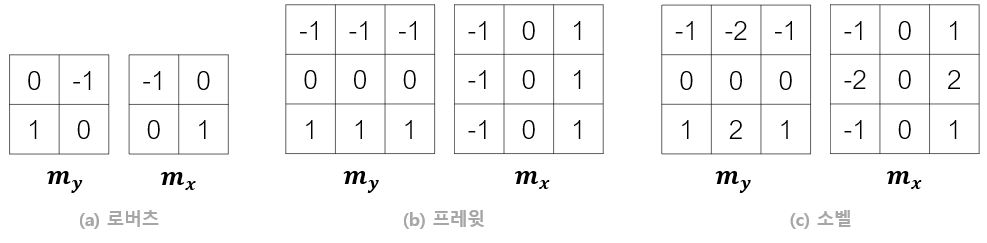
- 이중 소벨 연산자(Sobel Operator)와 프레윗 연산자(Prewitt Operator)는 해당 픽셀의 아래와 윗행까지 같이 고려한다.
- 즉, 스무딩 효과가 내포되어 있다. 게다가 소벨 연산자는 가까운 화소에 더 큰 가중치를 준다는 차이점이 존재한다.
1. Roberts Filter
- 커널 크기 : 2x2
- 장점 : 다른 마스크보다 크기는 작지만 효과적으로 사용할 수 있다.
- 단점 : 돌출 된 값을 평균에 적절히 활용하기 어렵다. 즉 잡음에 민감하다
2.Previtt Operator
- 커널 크기 : 3x3
- 장점 : 소벨 필터의 결과와 거의 같은 결과 값을 나타내는데
응답시간이 약간 빠르며, 돌출된 값을 비교적으로 효율적으로 평균화
- 단점 : 수평과 수직에 놓여진 에지에 민감하게 반응
윤곽선이 덜 부각되어 나타남
3.Sobel Filter
- 커널 크기 : 3x3
- 장점 : 원영상의 중심값을 더 강조한다, 돌출된 값을 평균화하는데 효율적이다.
대각선 방향에 놓여진 에지의 민감하게 반응
에지 강도와 에지 방향
-그레디언트는 벡터값이므로 에지 강도(edge strength)와 에지 방향(edge detection)을 구할 수 있다.

- 에지 강도는 화소 (y,x)가 에지일 가능성 또는 신뢰도를 나타내는 값이다.
가우시안과 다중 스케일 효과
- Edge Detection으로 Sobel filter를 주로 사용한다.
- 이 Sobel filter는 1차 미분 대신 2차 미분을 사용하였고, 미분을 적용하기 전에 가우시안으로 스무딩을 하는 전처리 과정을 중요하게 생각하였다.
Gaussian Smoothing은 두가지 효과를 제공한다.
1.잡음에 대처 가능하다.
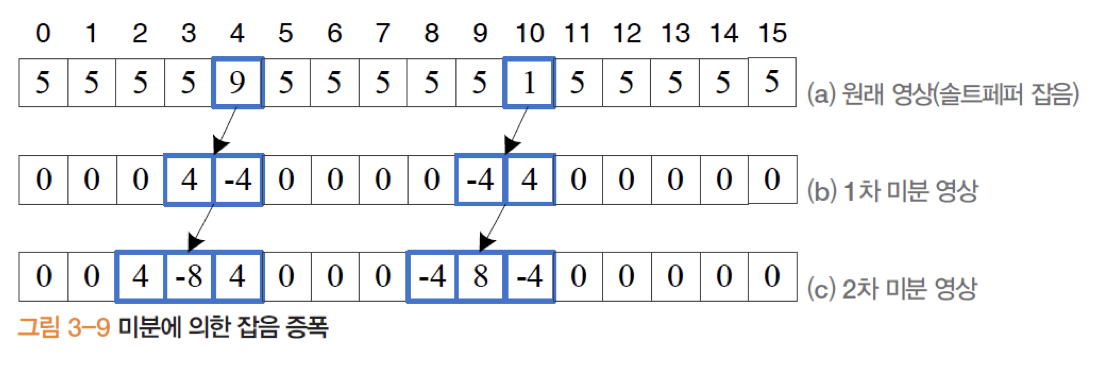
- 미분은 잡음을 증폭하므로 스무딩은 매우 중요하다.
- 특히 2차 미분은 미분을 두 번 수행하므로 잡음 증폭이 더욱 심하다.
2.가우시안의 매개변수 표준편차를 조절해 다중 스케일(multi- scale) 효과를 얻을 수 있다.

- 표준편차가 0.5일때 1차 미분과 2차 미분 결과를 살펴보면 물체의 크기와 상관없이 1차 미분에서 봉우리와, 2차 미분에서 영교차가 선명하게 나타난다.
- 하지만 표준편차가 커짐에 따라 폭이 작은 물체의 에지는 약해짐을 알 수 있다.
- 결론적으로 가우시안의 표준편차를 조절해 스무딩 정도를 조절할 수있고, 스무딩 정도는 에지 스케일을 정해준다는 것이다.
표준편차를 크게할수록 큰 물체의 에지만 검출, 작게할수록 물체와 디테일에 해당하는 에지까지 추출가능
- 가우시안 필터의 표준편차 값에 따라 엣지 영상이 잘 나올수도 있고 그렇지 않을 수도 있다.
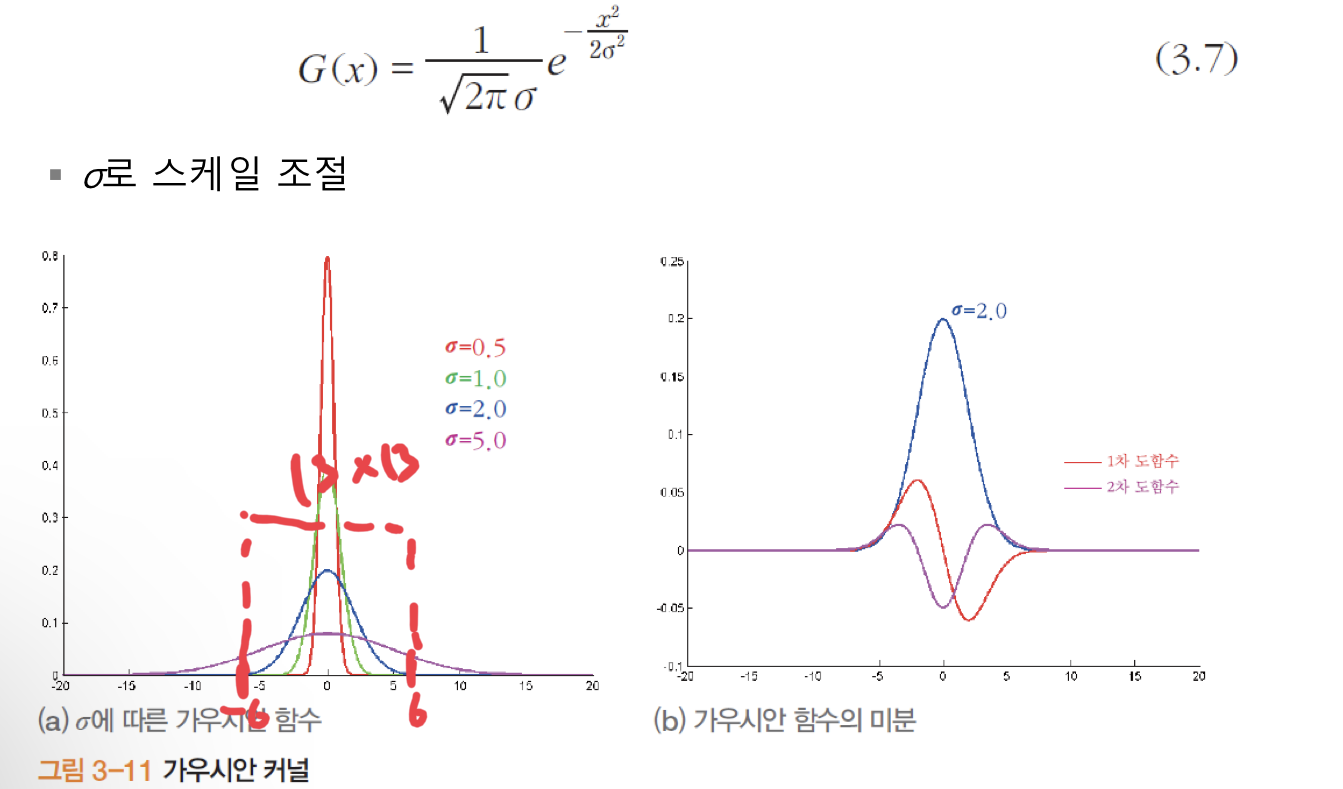
- 표준편차 값이 크면 우뚝 좌우로 넓게 퍼지며, 봉우리는 낮아진다.
- 즉, 표준편차가 클수록 가우시안의 영향력 범위는 넓다.
OpenCV를 통해 Gradient를 이용해 이미지의 edge 검출하기
1. cv2.Sobel()
- Gaussian smoothing과 미분을 이용한 방법이다.
- 그렇기에 노이즈가 있는 이미지에 적용하면 좋다.
cv2.Sobel(src, ddepth, dx, dy, dst=None, ksize=None, scale=None, delta=None, borderType=None) -> dst
• src: 입력 영상
• ddepth: 출력 영상 데이터 타입. -1이면 입력 영상과 같은 데이터 타입을 사용.
• dx: x 방향 미분 차수. 1차미분할지 2차미분 할지 결정
• dy: y 방향 미분 차수.
• dst: 출력 영상(행렬)
• ksize: 커널 크기. 기본값은 3.
• scale 연산 결과에 추가적으로 곱할 값. 기본값은 1.
• delta: 연산 결과에 추가적으로 더할 값. 기본값은 0.
• borderType: 가장자리 픽셀 확장 방식. 기본값은 cv2.BORDER_DEFAULT.
import cv2
import numpy as np
import matplotlib.pyplot as plt
src = cv2.imread('lena.png', cv2.IMREAD_GRAYSCALE)
# dx와 dy를 합쳐서 출력해야합니다.
dx=cv2.Sobel(src,cv2.CV_64F,0,1)
dy=cv2.Sobel(src,cv2.CV_64F,1,0)
#dx,dy 합친 이미지
src_edge = np.uint8(np.sqrt((dx**2)+(dy**2)))
plt.subplot(221),plt.imshow(np.uint8(abs(dx)))
plt.subplot(222),plt.imshow(np.uint8(abs(dy)))
plt.subplot(223),plt.imshow(src_edge)
plt.xlim([0,256])
plt.show()
2.cv2.Scharr()
- Gaussian smoothing과 미분을 이용한 방법이다.
- Sobel과 비슷하다
cv2.Scharr(src, ddepth, dx, dy, dst=None, scale=None, delta=None, borderType=None) -> dst
• src: 입력 영상
• ddepth: 출력 영상 데이터 타입. -1이면 입력 영상과 같은 데이터 타입을 사용.
• dx: x 방향 미분 차수
• dy: y 방향 미분 차수.
• dst: 출력 영상(행렬)
• scale 연산 결과에 추가적으로 곱할 값. 기본값은 1
• delta: 연산 결과에 추가적으로 더할 값. 기본값은 0.
• borderType: 가장자리 픽셀 확장 방식. 기본값은 cv2.BORDER_DEFAULT
3.cv2.Laplacian()
- 이미지의 가로와 세로에 대한 Gradient를 2차 미분한 값이다.
- 다. Sobel filter에 미분의 정도가 더해진 것과 비슷합니다.(dx와 dy가 2인 경우)
- blob(주위의 pixel과 확연한 picel차이를 나타내는 덩어리)검출에 많이 사용됩니다.

- 장점 :섬세한 에지 검출이 가능
모든 방향의 에지 검출이 가능
- 단점 : 잡음에 민감.
cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]]) → dst
- src - 입력 영상
- ddepth - 출력 영상 데이터 타입
Canny Edge
- 위에선 그래디언트 크기를 구하고 임계값을 설정해줘서 에지를 검출했다.
- 전에 보았던 것들은 모두 '그럴듯해 보이는' 에지 연산자를 설계하여 사용했다.
- 또한 윤곽선이 너무 두껍게 표현된다는 단점이 있다.
- 이를 보완한 것이 캐니 에지 검출 방법이다.
- 캐니는 기존의 파라미터를 대충 어림짐작하여 접근한 방식(휴리스틱-hueristic 이라고도 함)을 뛰어넘어 에지 검출을 최적화 문제로 취급하였다.
- 캐니는 좋은 에지 알고리즘이 갖추어야 할 세가지 기준을 제시하였다.
1. 정확한 검출 - Good detection
픽셀이 조명에 의해 미세한 영향을 받게 되어 임계점보다 크거나 낮아질 수 있습니다.
이처럼 에지가 아닌 점을 에지로 찾거나 또는 에지인데 에지로 찾지 못하는 확률을 최소화 한것을 정확한 검출이라고 합니다.
2. 정확한 위치 - Good localization
실제 에지의 중심을 검출하는 것입니다.
3. 단일 에지 - Single edge
하나의 에지는 하나의 점으로 표현한다는 것입니다.
이 세가지 조건을 충족해야 좋은 에지라고 할 수 있다.
- 캐니는 기준에 부합하믄 목적 함수를 만든 후, 이 함수를 최적화하는 연산자 설계를 시도하였다.
Canny Edge 검출 4단계
케니 에지 검출 방법은 4단계이다.
1. 가우시안 필터링
- 가우시안 필터링을 통해 잡음을 제거한다.
- 그레이언트 계산에서 소벨 마스크를 사용하므로 필터링은 선택적이다.
2. 그레디언트 계산
- 그레디언트 계산은 주로 소벨 마스크를 사용한다.
- 소벨 연산자를 적용하여 에지 강도와 에지 방향 맵을 구한다.
- 앞에 나온 그레디언트 계산에는 에지의 크기만 계산하여 윤곽선을 추출했지만, 캐니 에지의 경우 크기와 방향 모두 이용한다.

3. 비최대 억제
- 하나의 에지가 여러개의 픽셀로 표현되는 현상을 없애기 위해 그래디언트 크기가 국지적 최대인 픽셀만을 에지 픽셀로 설정한다.
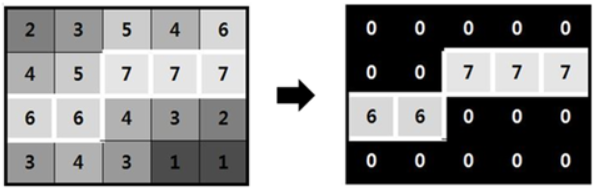
4.이력 임계값 적용하여 거짓 긍정 제거
- 거짓 긍정이란 실제로는 에지가 아닌데 어떤 이유에 의해 에지로 판정된 경우를 말한다.
- 이런 거짓 긍정을 제거할 수 있는 가장 간단한 방법은 임계값 T를 두어 화소 P에 대한 에지 강도가 T보다 작다면 거짓 긍정으로 간주하여 제거하는 것이다.
- 이때 하나를 얻으면 하나를 잃는 길항 작용(trade-off)이 발생하게 된다.
- T를 높게 작으면 거짓 긍정에 대한 제거가 잘되는 반면, 에지 강도가 낮은 진짜 에지까지 제거하는 거짓 부정 문제가 야기된다.
여기서 거짓 긍정, 거짓 부정은 전에 공부했던 Confusion Matrix를 의미한다. FP, FN
- 그렇기에 두개의 임계값(T-high, T-low)을 사용하여 거짓 긍정을 줄인다.
- 에지 추적은 T-high을 넘는 화소에서 시작한다. T-high보다 높으면 강한 에지가 되며, 항상 에지로 선정한다.
- T-high보다는 작고 T-low보다 높으면 약한 에지로 부르는데, 강한 에지와 이웃해 있으면 에지 강도가 낮더라도 에지로 선정된다.
- 하지만 T-high를 넘는 화소가 이웃해 있더라도 T-low 보다작으면 에지로 선정하지 않는다.
- 캐니는 T-high를 T-low의 2~3배로 할것을 권고한다.
2. Edge Detection
- edge는 영상의 명암도를 기준으로 명암의 변화가 큰 지점이다.
- 따라것 명암, 밝기 변화율 즉 기울기를 검출해야 한다.
- 이러한 기울기의 검출 방법이 바로 1차 미분이다.
- Image Gradient를 이용해 경계선을 구하는 Edge Detection 분야에는 Sobel, LOG, Canny등이 있다
- 거의 대부분 Gaussian smoothing과 미분을 이용한 방법이므로 노이즈가 있는 이미지에 적용하면 좋다.
Canny Edge 검출 함수 - cv2.Canny
cv2.Canny(image, threshold1, threshold2, edges=None, apertureSize=None, L2gradient=None) -> edges
• image: 입력 영상
• threshold1: 하단 임계값
• threshold2: 상단 임계값
• edges: 에지 영상
• apertureSize: 소벨 연산을 위한 커널 크기. 기본값은 3
• L2gradient: True이면 L2 norm 사용, False이면 L1 norm 사용. 기본값은 False.
- 하단 임계값과 상단 임계값은 실험상으로 결정해야 한다.
- L2gradient인자에서 L2 norm이 L1 norm보다 정확하지만 연산이 오래걸려 속도가 느리다.
- L1 norm(기본값)을 주로 이용합니다.
- 주의할 점은 입력 영상에 그레이스케이 영상을 입력해주는 것이 좋다.
- 컬러 영상을 입력할 시에 RGB픽셀 따로따로 캐니해서 최댓값을 검출하므로 가급적으로 그레이스케일 영상으로 입력하는 것이 좋다.
src = cv2.imread('building.jpg', cv2.IMREAD_GRAYSCALE) # 그레이 스케일 영상
if src is None:
print('Image load failed!')
sys.exit()
dst = cv2.Canny(src, 50, 150) # 하단 임계값과 상단 임계값은 실험적으로 결정하기
cv2.imshow('src', src)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()

허프 변환에 의한 선분 검출 함수 - cv2.HoughLines
- 캐니 함수로 윤곽선을 검출한 값을 cv2.HoughLines에 입력 값으로 설정하면 직선 파라미터 정보를 담고 있는 결과값을 반환한다.
cv2.HoughLines(image, rho, theta, threshold, lines=None, srn=None, stn=None, min_theta=None, max_theta=None) -> lines
• image: 입력 에지 영상
• rho: 축적 배열에서 rho 값의 간격. (e.g.) 1.0 → 1픽셀 간격
• theta: 축적 배열에서 theta 값의 간격. (e.g.) np.pi / 180 → 1픽셀 간격
• threshold: 축적 배열에서 직선으로 판단할 임계값
• lines: 직선 파라미터(rho, theta) 정보를 담고 있는 numpy.ndarray. shape=(N, 1, 2). dtype=numpy.float32.
• srn, stn: 멀티 스케일 허프 변환에서 rho 해상도, theta 해상도를 나누는 값. 기본값은 0이고, 이 경우 일반 허프 변환 수행.
• min_theta, max_theta: 검출할 선분의 최소, 최대 theta 값
- rho값과 theta값의 간격은 축적 배열을 만들 때 rho값 해당 축과 theta 해당 축의 크기를 몇으로 설정할 것인지를 의미한다.
- 이 값을 작게 하면 축적 배열이 커집니다. (연산이 오래 걸리지만 정교합니다)
- 간격을 크게 하면 축적배열은 작아진다. (연산은 빠르지만 정밀도가 떨어집니다.)
- lines 결과값은 3차원 형상으로 반환한다.
(N, 1, 2)에서 1은 값이 비어있다.
import cv2
import numpy as np
img = cv2.imread('./line.png')
img_original = img.copy()
edges = cv2.Canny(img,50,150)
e1 = cv2.getTickCount()
lines = cv2.HoughLines(edges,1,np.pi/180,150)
e2 = cv2.getTickCount()
t = (e2 - e1) / cv2.getTickFrequency()
for i in range(len(lines)):
for rho, theta in lines[i]:
a = np.cos(theta); b = np.sin(theta)
x0 = a*rho; y0 = b*rho
x1 = int(x0 + 1000*(-b)); y1 = int(y0+1000*(a))
x2 = int(x0 - 1000*(-b)); y2 = int(y0-1000*(a))
cv2.line(img,(x1,y1),(x2,y2),(0,0,255),5)
res = np.vstack((img_original,img))
cv2.imshow('img',res)
cv2.imshow('edges',edges)
print('time:',t)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.waitKey(0)
허프 변환에 의한 선분 검출 함수 - cv2.HoughLines
- 허프 변환과의 차이점은 결과값 lines의 파라미터가 다르다.
- 허프 변환 함수는 로우와 세타 값으로 직선의 파라미터 정보를 제공했지만
- 확률적 허프 변환 함수는 직선의 시작과 끝 정보를 제공합니다.
cv2.HoughLinesP(image, rho, theta, threshold, lines=None, minLineLength=None, maxLineGap=None) -> lines
• image: 입력 에지 영상
• rho: 축적 배열에서 rho 값의 간격. (e.g.) 1.0 → 1픽셀 간격
• theta: 축적 배열에서 theta 값의 간격. (e.g.) np.pi / 180 → 1픽셀 간격.
• threshold: 축적 배열에서 직선으로 판단할 임계값
• lines: 선분의 시작과 끝 좌표(x1, y1, x2, y2) 정보를 담고 있는 numpy.ndarray. shape=(N, 1, 4). dtype=numpy.int32.
• minLineLength: 검출할 선분의 최소 길이
• maxLineGap: 직선으로 간주할 최대 에지 점 간격
- 주의할 점은 maxLineGap 인자이다. 디폴트 값은 0이지만 0보다 큰 값을 주는 것이 좋다.
- 조명이나 외부 변수에 의해 픽셀값이 변화되서 직선이 끊길 수 있다.
- 0은 한 픽셀 떨어져도 끊는데 5는 5픽셀 정도 떨어져도 직선을 붙인다. 5이상 줘야 함
import cv2
import numpy as np
img = cv2.imread('./line.png')
img_original = img.copy()
edges = cv2.Canny(img,50,150)
minLineLength = 10
maxLineGap = 100
e1 = cv2.getTickCount()
lines = cv2.HoughLinesP(edges,1,np.pi/180,100,minLineLength,maxLineGap)
e2 = cv2.getTickCount()
t = (e2 - e1) / cv2.getTickFrequency()
for i in range(len(lines)):
for x1,y1,x2,y2 in lines[i]:
cv2.line(img,(x1,y1),(x2,y2),(0,0,255),5)
res = np.vstack((img_original,img))
cv2.imshow('img',res)
print('time:',t)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.waitKey(0)